Basic Linear Regression Model Example

Ben Woodard November 18, 2025
r bayesian marketing

The workhorse of all data science work is the basic linear regression model. It has the capability to change the direction of a business like a rudder on a boat but like a rudder, it is often overlooked by most practicioners until other more ‘advanced’ tactics are tried.

Here is an example of a basic bayesian linear regression model in R and stan.

Simulating the data is pretty straight forward.

set.seed(123)
N <- 100
x <- rnorm(N, 0, 1)

alpha_true <- 2.5
beta_true  <- 0.8
sigma_true <- 1.0

y <- alpha_true + beta_true * x + rnorm(N, 0, sigma_true)

df <- data.frame(x, y)
head(df)
            x        y
1 -0.56047565 1.341213
2 -0.23017749 2.572742
3  1.55870831 3.500275
4  0.07050839 2.208864
5  0.12928774 1.651812
6  1.71506499 3.827024

Now that we have the data we want to create a linear regression model that shows the results of

lm_fit <- lm(y ~ x, data = df)
summary(lm_fit)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.9073 -0.6835 -0.0875  0.5806  3.2904 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.39720    0.09755  24.574  < 2e-16 ***
x            0.74753    0.10688   6.994  3.3e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9707 on 98 degrees of freedom
Multiple R-squared:  0.333, Adjusted R-squared:  0.3262 
F-statistic: 48.92 on 1 and 98 DF,  p-value: 3.304e-10

Key parts of summary(lm_fit):

confint(lm_fit)
                2.5 %    97.5 %
(Intercept) 2.2036098 2.5907841
x           0.5354312 0.9596255

Interpretation (frequentist):

If we repeated this estimation procedure infinitely many times, 95% of the constructed intervals would contain the true parameter.

(Contrast: in Bayesian, you’d say “there’s a 95% probability the parameter lies in this interval, given data + priors.”)

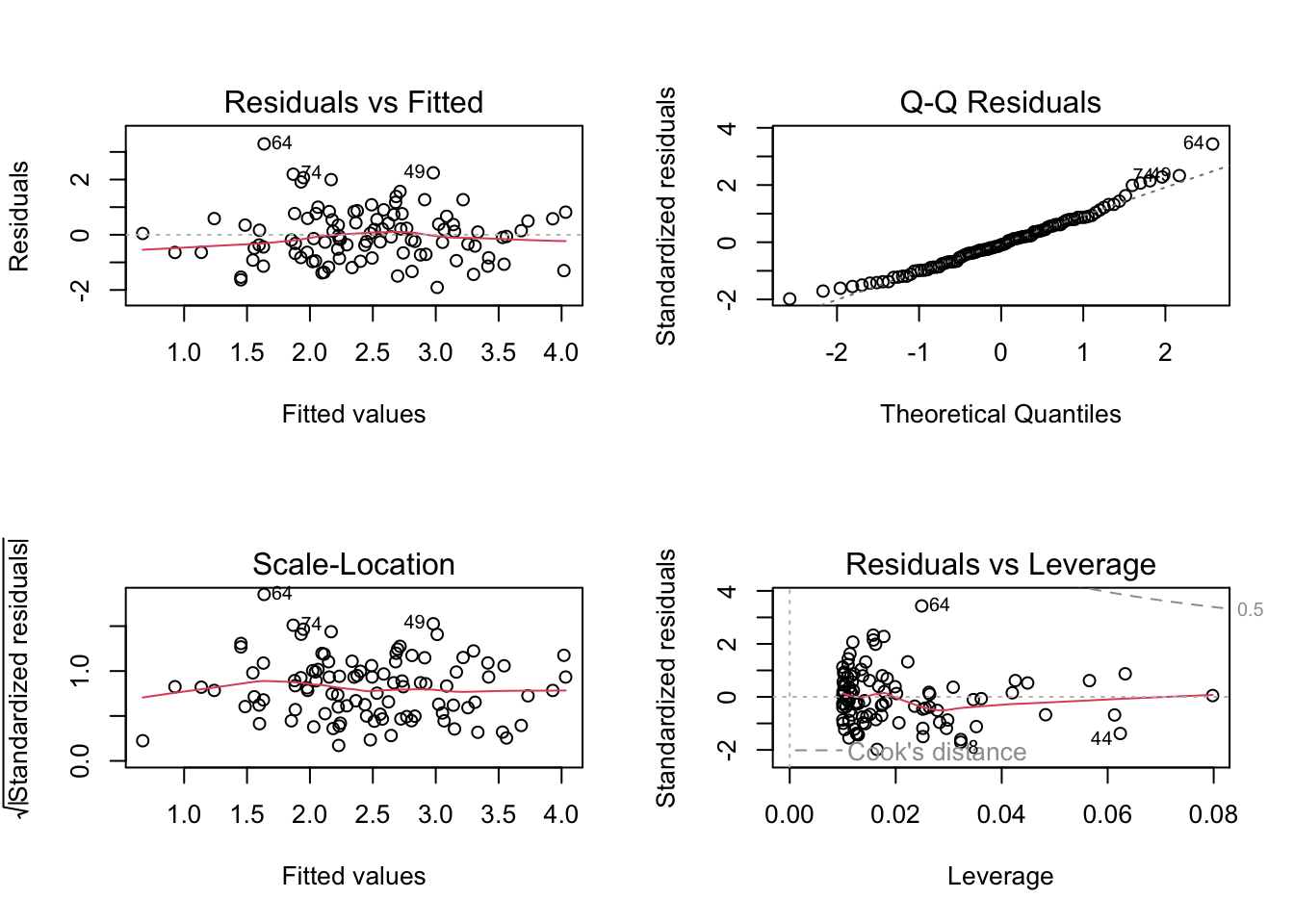
Basic Diagnostic Plots

par(mfrow = c(2, 2))
plot(lm_fit)

par(mfrow = c(1, 1))

You get:

  • Residuals vs Fitted (linearity, homoskedasticity)
  • Normal Q-Q (normality of residuals)
  • Scale-Location
  • Residuals vs Leverage (influence)

Predictions with confidence & prediction intervals

new <- data.frame(x = seq(-2, 2, length.out = 30))

# Confidence interval for the *mean* response
pred_conf <- predict(lm_fit, newdata = new, interval = "confidence", level = 0.95)

# Prediction interval for a *new* observation
pred_pred <- predict(lm_fit, newdata = new, interval = "prediction", level = 0.95)

head(pred_conf)
        fit       lwr      upr
1 0.9021402 0.4187310 1.385549
2 1.0052475 0.5485212 1.461974
3 1.1083549 0.6779769 1.538733
4 1.2114623 0.8070330 1.615892
5 1.3145696 0.9356071 1.693532
6 1.4176770 1.0635953 1.771759
head(pred_pred)
        fit        lwr      upr
1 0.9021402 -1.0839403 2.888221
2 1.0052475 -0.9745075 2.985003
3 1.1083549 -0.8654881 3.082198
4 1.2114623 -0.7568858 3.179810
5 1.3145696 -0.6487041 3.277843
6 1.4176770 -0.5409462 3.376300
  • “confidence” = uncertainty about E[y | x]
  • “prediction” = uncertainty about a new y at that x (includes residual noise, so wider)
library(ggplot2)

pred_df <- cbind(new, as.data.frame(pred_conf))
names(pred_df) <- c("x", "fit", "lwr", "upr")

# ggplot(df, aes(x, y)) +
#   geom_point(alpha = 0.7) +
#   geom_line(data = pred_df, aes(x, fit)) +
#   geom_ribbon(
#     data = pred_df,
#     aes(x = x, ymin = lwr, ymax = upr),
#     alpha = 0.2
#   ) +
#   labs(
#     title = "Frequentist Linear Regression (lm)",
#     subtitle = "Fitted line with 95% confidence band for mean response"
#   )
  1. Quick contrast with your Bayesian version Using the same simulated data:
  • Frequentist (lm):
    • Coefficients: point estimates + SE
    • 95% CIs: coverage interpretation over repeated samples
    • p-values: H₀ tests (β = 0, etc.)
  • Bayesian (stan_glm):
    • Coefficients: full posterior distributions
    • 95% intervals: “credible intervals” (probability statements given model + priors)
    • No p-values; you might instead look at Pr(β > 0) or posterior density.